Zusammenhang zwischen Strom, Spannung und Widerstand

Nichtlineare Widerstände, grafische Darstellung

Es gibt eine Vielzahl von elektronischen Bauelementen bei denen der Widerstand von einer weiteren physikalischen Größe Abhängig ist. Diese kann die Eigenerwärmung auf Grund des durchfließenden Stroms, aber auch eine Veränderung des Leitwertes in Abhängigkeit von der anliegenden Spannung sein. Die Widerstandsänderung kann aber auch durch Magnetfelder, Temperatur, Licht und vieles mehr verändert werden. Solche Bauelemente werden als Sensoren bezeichnet. Der Zusammenhang zwischen Strom und Spannung ist nicht linear, sondern von einem Parameter (Nebenmessung) abhängig.

Der Zusammenhang zwischen Strom und Spannung  eines Bauelements mit nichtlinearem Kennlinienverlauf kann entweder rein mathematisch durch Formeln, oder für den nicht geübten Mathematiker grafisch dargestellt werden. Diese kommt für uns in erster Linie in Frage.

Der Zusammenhang zwischen Strom, Spannung und Widerstand eines nichtlinearen Widerstandes kann für die Praxis (nur) graphisch dargestellt werden.

Ist der Widerstand nicht konstant, sind Strom und Spannung zueinander nicht proportionale Größen. Der Zusammenhang kann durch eine Funktionsgleichung höherer Ordnung dargestellt werden. Diese Gleichung beschreibt den Strom I als Funktion der Spannung U in Abhängigkeit mindestens einer Variablen.

Der Graph der Funktion I = f(U) ergibt eine Widerstandskennlinie, welche keine Gerade ist. Der Widerstandswert R des Bauelementes ändert sich von Punkt zu Punkt der Kennlinie und muss jeweils mit R = U/I berechnet werden.

Für eine große Spannungsänderung kann der zu erwartende Strom nicht berechnet werden. Er kann nur aus der Kennlinie abgelesen werden.

Für eine sehr kleine Spannungsänderung kann die Kennlinie in diesem Bereich mit großer Genauigkeit als Gerade (Tangente) angenommen werden, deren Steigung  ist. Der Kehrwert der Steigung  ist ein Widerstandswert und wird als differentieller Widerstand bezeichnet.

Das Formelzeichen des differentiellen Widerstandes ist r.  

Die Einheit des differentiellen Widerstandes ist Ohm (W).

r

Differentieller Widerstand

U₁, U₂

Spannungen verschiedener Arbeitspunkte

I₁, I₂

Stöme verschiedener Arbeitspunkte

DU

 Spannungsdifferenz

DI

Stromdifferenz

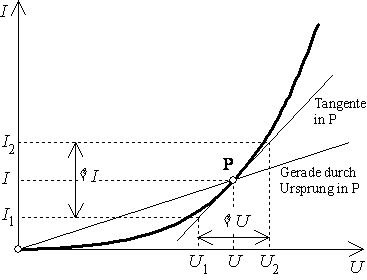
Die Steigung der Geraden durch den Ursprung ist ein Maß für den Widerstand R.

Die Steigung der Tangente ist ein Maß für den differentiellen Widerstand r.

Für Widerstände mit nicht linearem Verlauf kann die zu erwartende Stromänderung für eine sehr kleine Spannungsänderung mit Hilfe des differentiellen Widerstandes r berechnet werden.